La conocida sucesión de Fibonacci es aquella sucesión que comienza con los términos 0 y 1, y continua obteniendo cada término sumando sus dos anteriores. Mas formalmente:

En este orden de ideas, es fácil descubrir los primeros términos de la sucesión: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, .... Del mismo modo podemos expresar cada termino en base a su función: fib(0) = 0, fib(1) = 1, fib(2) = 1, fib(3) = 2, fib(4) = 3, fib(5) = 5...

Dada esta definición formal, no es nada difícil crear una primera solución recursiva para obtener un término n de la sucesión de Fibonacci:

FUNCTION fibonacci (INTEGER n)
     IF (n < 2) RETURN n
     ELSE
          RETURN fibonacci(n - 1) + fibonacci(n - 2)

Pero analicemos a fondo lo que hace esta función. Recursivamente, estará llamando a sus dos anteriores. Cada una de estas llamadas, si es mayor que 1, de nuevo estará llamando a sus dos anteriores. Analicemos el árbol de llamadas para un fibonacci de orden 6:

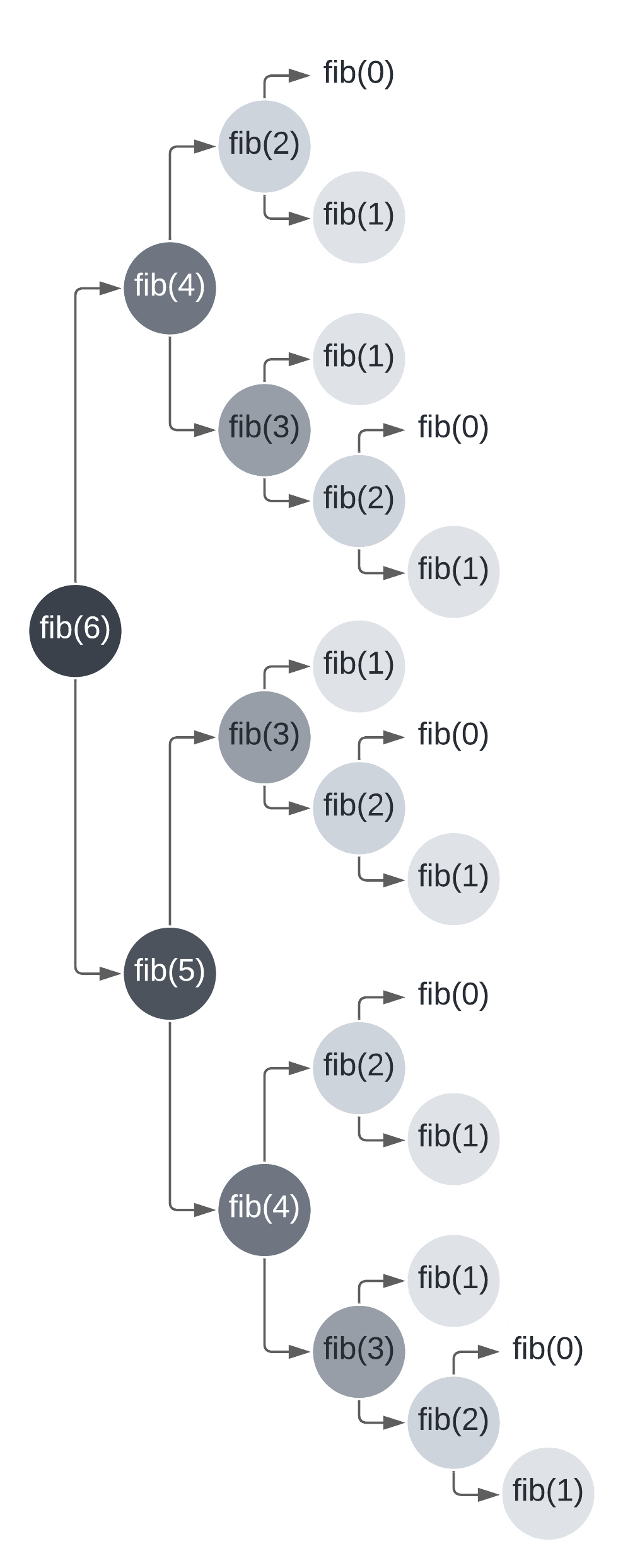
Este es un algoritmo de orden exponencial, mas exactamente φ^n. La explicación de este costo puede ser algo extensa, así que si quieres leerla a fondo, te recomiendo esta explicación (páginas 11/12). Esto significa que es terriblemente lento, pues tendrá que hacer excesivas operaciones para valores altos de n.

¿A que se debe esta ineficiencia?

Volvamos al árbol. Para calcular una vez fib(6), es necesario calcular una vez fib(5), dos veces fib(4), tres veces fib(3), cinco veces fib(2), ocho veces fib(1) y cinco veces fib(0) (Como el algoritmo considera constante fib(1), solo tenemos cinco llamadas a fib(0). Si fib(1) se calculara con su antecesor, tendríamos 13 llamadas). ¡Estamos repitiendo operaciones! Y lo peor, estas operaciones se repiten justamente siguiendo la secuencia de Fibonacci como se puede ver en los números en negrilla (1,1,2,3,5,8,13).

¿Como podemos mejorarlo?

Si eliminamos los cálculos repetidos, fácilmente podemos tener un algoritmo de O(n). Para hacer esto, utilizaremos un array que guarde los valores calculados para hallar el siguiente valor:

FUNCTION fibonacci (ARRAY [n + 1] terminos, INTEGER n)
     IF (n < 2)
          RETURN n
     ELSE
          terminos[0] = 0
          terminos[1] = 1
          FOR(INTEGER i IN RANGE [2, n])
                terminos[i] = terminos[i - 1] + terminos[i - 2]
          RETURN T[n]

Ahora el algoritmo es mucho mas eficiente, reduciendo enormemente el número de operaciones innecesarias para valores altos de n. Pero surge un nuevo problema. La complejidad espacial es de O(n) también. Hemos sacrificado espacio por tiempo, ahora tenemos un array de n posiciones cuando en realidad solo necesitábamos la posición n y las demás podemos desecharlas.

Como el algoritmo ÚNICAMENTE necesita de los dos valores anteriores para obtener el siguiente, podemos evitar el array, y así reducir su espacio ocupado:

Reduciendo costo espacial

FUNCTION fibonacci(INTEGER n)
    INTEGER a = 0, b = 1, c
    FOR(INTEGER i = 0; i < n; i++)
        c = a + b
        a = b
        b = c
    RETURN a

Ahora la complejidad temporal sigue siendo de orden O(n) pero la complejidad espacial se reduce a un orden O(1)

¿Que tal un algoritmo O(log2n)?

Volviendo al inicio, sabemos que:

Partiendo de aquí, podemos desarrollar un sistema de ecuaciones:

Lo cual podemos llevar a una ecuación matricial:

Reemplazando n=2:

Conociendo que fib(0) = 0 y fib(1) = 1:

Y efectivamente, fib(2) = 1. Ahora bien, generalizando para diferentes valores de n:

Ahora recordemos 3 propiedades de la potenciación:

Los cuales nos permitirán hacer un “divide y vencerás” para resolver la potencia de una manera eficiente:

Ahora si, procedemos al algoritmo:

FUNCTION fibonacci(INTEGER n)
     INTEGER h, i, j, k, aux
     h = i = 1
     j = k = 0
     WHILE (n > 0)
         IF ( n % 2 != 0)
             aux = h * j
             j = (h * i) + (j * k) + aux
             i = (i * k) + aux
         aux = (h * h)
         h = (2 * h * k) + aux
         k = (k * k) + aux
         n = n / 2
     RETURN j

¿Que demonios he hecho? Básicamente, partir el problema. Para explicarlo, miremos paso a paso el proceso para hallar el fib(11):

Y así llegamos a la respuesta de manera mas rápida, en un orden O(log2n). Para hacernos una idea, para calcular el fib(200) con el algoritmo exponencial, ocuparíamos 6.2737x10^41 cálculos (no terminaría nunca). Con el algoritmo de orden O(n) ocuparíamos 200 cálculos, y con este algoritmo, 8 cálculos. Por supuesto no significa que el computador solo realice 8 operaciones, ya que cada uno de estos cálculos conlleva alguna cantidad de sub-calculos asociados. Pero todos son subcalculos constantes y despreciables, y por tanto la diferencia es abismal.

Una última mejora

Ok ok, esto no es una última mejora, en realidad es un cambio total. Hasta ahora hemos manejado cada término de la sucesión en base a sus términos anteriores. Pero existe también una formula explicita creada por Edouard Lucas para hallar directamente un término sin necesidad de iterar.

Partiendo de esta formula, podemos crear esta función:

FUNCTION fibonacci(int n)
    DOUBLE raiz = sqrt(5)
    DOUBLE rta = ((1 / raiz) * (pow((1 + raiz) / 2, n)) - (1 / raiz)*(pow((1 - raiz) / 2, n)))
    RETURN ROUND(rta)

Esta función es muy eficiente, pero su orden depende de la manera de implementar la potenciación. Una potenciación por cuadrados como en el caso anterior, arroja un costo de O(log2n). La mayoría de lenguajes tienen funciones optimizadas para estos calculos, pero en cualquier caso siempre existe la posibilidad de implementar nuestra propia potenciación.

Algunas generalidades

• En muchos sitios, incluso textos es común leer “serie Fibonacci”. Esto es un error, fibonacci es una sucesión, no una serie. Una sucesión es un conjunto de elementos con cierto orden, la serie por su parte es la suma de los términos de una sucesión.

• La sucesión de Fibonacci crece rápidamente, así que si van a calcularse valores muy altos, deben tomarse las medidas necesarias para evitar que exceda el tamaño del tipo de datos indicado.

• El verdadero nombre del ideador de la sucesión es Leonardo de Pisa, no Fibonacci. Este sobrenombre viene de su padre quien era apodado “Bonacci” (Bien intencionado), y se convierte en Filius Bonacci (Hijo de Bonacci) que termina siendo reducido a Fibonacci.

Si encuentras algún error en esta publicación (lo cual es muy posible dado la cantidad de números, matrices y códigos que contiene) puedes avisarme aqui. ¡Muchas gracias!

La foto que acompaña este artículo fue compartida por Roman Mager en Unsplash.